Д.А. Тучин Кодовые измерения псевдодальности системы GPS. Модель ошибок и
априорная оценка точности определения вектора положения
2.2. Определение точности измерений псевдодальности из условия
соответствия фактической точности ее априорной оценке
В силу линейности
(2.1.)можно записать соотношение для измерения от i-го НКА:
(2.3)
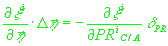 , ,
где 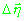 - вектор неизвестных параметров
(1.3.), - вектор неизвестных параметров
(1.3.),
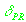 - ошибка измерения псевдодальности. - ошибка измерения псевдодальности.
Для n изохронных измерений соотношение (2.3) перепишем
в матричной форме:
(2.4)
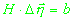 , (2.4) , (2.4)
где 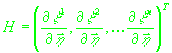 , ,
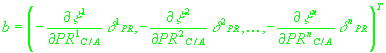 . .
Ковариационная матрица ошибок определения неизвестных параметров
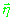 имеет вид
[6]: имеет вид
[6]:
(2.5)
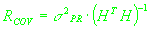 . .
Рассмотрим корреляционные связи неизвестных компонент вектора положения.
Ковариационная матрица третьего порядка будет иметь вид
(2.5). Используя представление для симметричной матрицы в виде произведения
ортогональной матрицы, диагональной матрицы и транспонированной первой матрицы,
можно представить ковариационную матрицу третьего порядка в следующем виде:
(2.6)
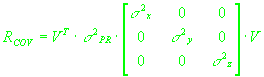 , ,
где  - ортогональная матрица. Для построения такого
разложения был использован симметричный GR-алгоритм
[5]. - ортогональная матрица. Для построения такого
разложения был использован симметричный GR-алгоритм
[5].
При обработке каждой группы одновременных кодовых измерений базовых GPS-станций
вычислялся вектор ошибки определения положения наблюдателя
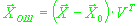 , где , где
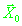 - априорно известный точный вектор положения.
Затем находилось такое значение - априорно известный точный вектор положения.
Затем находилось такое значение
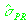 , при котором вектор ошибки , при котором вектор ошибки
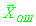 попадал на границу эллипса попадал на границу эллипса
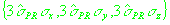 . Таким образом, для каждой группы изохронных измерений
искалось такое значение ошибки измерения псевдодальности, которое удовлетворяет
следующему соотношению: . Таким образом, для каждой группы изохронных измерений
искалось такое значение ошибки измерения псевдодальности, которое удовлетворяет
следующему соотношению:
(2.7)
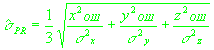 . .
В таблице 2.3. представлены фактическое (СКО,
таблица 2.1.) и
априорное (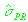 ) значение ошибки измерения псевдодальности
для 17 дней обработанных измерений. В последней строке представлены среднее
фактическое и априорное значения ошибок для месячного интервала обработанных
измерений. ) значение ошибки измерения псевдодальности
для 17 дней обработанных измерений. В последней строке представлены среднее
фактическое и априорное значения ошибок для месячного интервала обработанных
измерений.
| |
bahr |
cena |
usno |
| |
СКО |
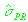 |
СКО |
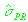 |
СКО |
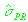 |
| 1 |
1.5 |
0.74 |
3.6 |
2.11 |
1.7 |
0.96 |
| 2 |
2.2 |
0.82 |
3.5 |
1.96 |
1.9 |
1.04 |
| 3 |
2.4 |
0.82 |
3.5 |
1.95 |
2.0 |
1.07 |
| 4 |
2.3 |
0.77 |
3.4 |
1.94 |
1.8 |
0.97 |
| 5 |
2.3 |
0.75 |
3.4 |
1.90 |
1.9 |
1.03 |
| 6 |
1.5 |
0.71 |
3.5 |
1.95 |
2.1 |
1.10 |
| 7 |
2.7 |
0.82 |
3.4 |
1.95 |
1.9 |
1.05 |
| 8 |
2.7 |
0.84 |
3.4 |
1.94 |
2.0 |
1.09 |
| 9 |
1.9 |
0.80 |
7.9 |
2.48 |
2.2 |
1.16 |
| 10 |
1.9 |
0.71 |
30.6 |
6.12 |
2.2 |
1.16 |
| 11 |
2.1 |
0.76 |
3.3 |
1.89 |
2.3 |
1.24 |
| 12 |
1.5 |
0.73 |
3.3 |
1.86 |
2.0 |
1.11 |
| 13 |
1.5 |
0.73 |
3.3 |
1.84 |
1.6 |
0.84 |
| 14 |
3.0 |
0.75 |
7.3 |
2.49 |
1.7 |
0.95 |
| 15 |
2.4 |
0.79 |
29.5 |
5.93 |
1.8 |
0.99 |
| 16 |
2.7 |
0.89 |
7.4 |
2.47 |
2.5 |
1.18 |
| 17 |
2.1 |
0.82 |
28.8 |
6.30 |
2.2 |
1.17 |
| |
2.6 |
0.84 |
12.6 |
2.66 |
2.0 |
1.08 |
Таблица 2.3.
Априорная и апостериорная оценки точности измерений псевдодальности
Назад |
Оглавление |
Далее
Версия PDF:
ftp://ftp.kiam1.rssi.ru/pub/gps/lib/publications/preprint30_02.pdf
|