2. Априорные оценки точности

     Исследованные в п.1 составляющие ошибок измерения псевдодальности, позволяют построить статистическую модель ошибки измерения псевдодальности, а на ее основе провести априорную оценку точности определения вектора положения.

2.1. Статистическая модель ошибок измерений псевдодальности

     Перепишем соотношение (1.2) в виде:

(2.1)     .

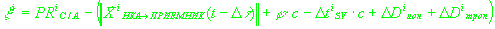     Определенные таким образом невязки 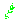будем интерпретировать как аппаратные ошибки измерения псевдодальности. Для определения невязок уточнялись два параметра: неизвестная фаза 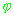генерации C/A последовательности и точность времени регистрации сигнала 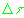. Вектор положения наблюдателя являлся априорно известным. Для более точного определения невязок использовались эталонные эфемериды и значения ухода часов НКА, тем самым была устранена ошибка эфемеридного и частотно-временного обеспечения.

     В таблице 2.1. представлены статистические характеристики невязок модели измерений псевдодальности на C/A коде на интервале 17 дней. Для каждой станции в таблице отражены минимальное, максимальное, среднее значения невязки, а также СКО и процент невязок, которые лежат внутри трех СКО. В последней строке показаны статистические характеристики для месячной базы обработанных измерений. Ошибки измерения псевдодальности не имеют систематики (среднее 0), приемники ASHTECH Z-X113 (bahr) и AOA SNR-12 ACT (usno) имеют ошибку измерения порядка 2 м, что более чем в два раза лучше, чем у приемника TRIMBLE 4000 SSI.

	bahr					cena					usno
	min	max	ср.	ско		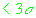min	max	ср.	ско		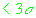min	max	ср.	ско
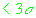1	-21.4	27.2	0.0	1.5	99.6	-18.9	29.3	0.0	3.6	97.9	-10.0	10.4	0.0	1.7	98.5
2	-19.8	83.1	0.0	2.2	99.4	-21.4	20.9	0.0	3.5	98.2	-15.1	18.8	0.0	1.9	98.3
3	-23.3	111.6	0.0	2.4	99.5	-21.1	24.9	0.0	3.5	98.0	-15.8	23.5	0.0	2.0	98.4
4	-35.3	195.1	0.0	2.3	99.7	-20.7	21.1	0.0	3.4	98.1	-16.8	16.5	0.0	1.8	98.5
5	-25.5	147.8	0.0	2.3	99.7	-23.2	23.7	0.0	3.4	98.0	-18.3	13.0	0.0	1.9	98.3
6	-27.8	70.3	0.0	1.5	99.5	-21.2	18.8	0.0	3.5	98.2	-15.8	16.4	0.0	2.1	98.2
7	-19.3	136.5	0.0	2.7	99.5	-23.4	23.4	0.0	3.4	98.2	-15.0	14.3	0.0	1.9	98.2
8	-25.4	142.4	0.0	2.7	99.5	-18.6	26.2	0.0	3.4	98.2	-15.4	17.1	0.0	2.0	98.1
9	-19.3	93.7	0.0	1.9	99.6	-39.6	39.9	0.0	7.9	97.6	-21.8	12.7	0.0	2.2	97.8
10	-21.5	138.6	0.0	1.9	99.7	-103.9	85.5	0.0	30.6	100.0	-18.7	11.5	0.0	2.2	98.2
11	-23.6	156.3	0.0	2.1	99.7	-17.1	20.0	0.0	3.3	98.6	-19.0	12.8	0.0	2.3	97.8
12	-18.5	38.0	0.0	1.5	99.4	-19.0	18.0	0.0	3.3	98.4	-15.9	14.9	0.0	2.0	98.3
13	-20.1	84.7	0.0	1.5	99.6	-20.1	22.8	0.0	3.3	98.3	-6.4	14.8	0.0	1.6	99.0
14	-28.0	217.5	0.0	3.0	99.6	-35.0	35.7	0.0	7.3	97.7	-14.2	12.5	0.0	1.7	98.4
15	-26.9	151.1	0.0	2.4	99.6	-99.6	84.5	0.0	29.5	100.0	-13.1	15.9	0.0	1.8	98.4
16	-27.3	95.4	0.0	2.7	99.4	-42.5	35.3	0.0	7.4	98.0	-24.1	13.6	0.0	2.5	98.5
17	-21.1	88.0	0.0	2.1	99.5	-113.1	88.3	0.0	28.8	99.8	-19.6	13.8	0.0	2.2	97.8
	-61.3	242.5	0.0	2.6	99.4	-113.1	92.9	0.0	12.6	96.5	-24.1	23.5	0.0	2.0	98.3

Таблица 2.1. Статистические характеристики невязок измерения псевдодальности

     Для описания статистической модели ошибок измерений псевдодальности было взято семейство распределений с плотностью вида:

(2.2)     ,

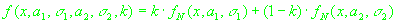где 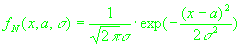- плотность нормального распределения.

     Поиск неизвестных параметров 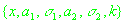распределения (2.2) проводился методом наименьших квадратов [6]. Проверка гипотезы о законе распределения проводилась с использованием критерия согласия хи-квадрат.

     Найденные плотности распределения для каждой GPS-станции изображены на рис. 2.1, а их параметры представлены в таблице 2.2.

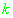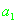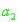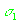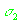bahr	0.335	-1.275	0.668	0.762	0.810
cena	0.295	-5.850	0.398	12.081	2.335
usno	0.110	-4.520	0.270	6.060	1.320

Таблица 2.2. Параметры распределения плотности ошибок измерений псевдодальности

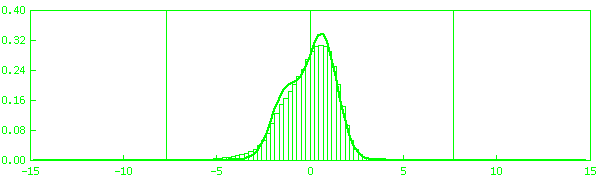
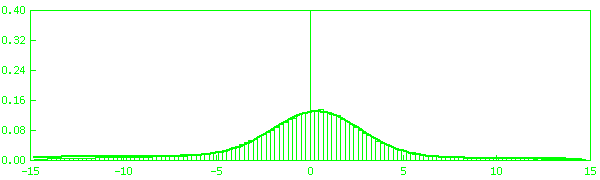
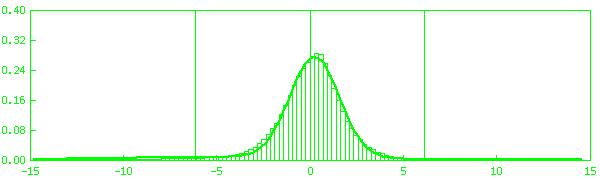
Рис. 2.1. Гистограмма и плотность распределения ошибок измерений псевдодальности а) bahr, б) cena, с) usno

     Из таблицы определения параметров распределения 2.2 видно, что процесс измерения псевдодальности различными типами приемников осуществляется по-разному. Это объясняется наличием у приемников различных алгоритмов деления измеряемого бита C/A кода.

Назад | Оглавление | Далее

Версия PDF: ftp://ftp.kiam1.rssi.ru/pub/gps/lib/publications/preprint30_02.pdf