Э.Л. Аким, Д.А. Тучин Апостериорная оценка точности определения вектора состояния земного
наблюдателя по измерениям дальности и скорости системы космической навигации
GPS
4. Алгоритм определения вектора состояния наблюдателя по данным измерений псевдодальности и псевдоскорости
Обозначим через
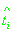 фактическое время приема сигнала от i-го НКА, которое отличается от шкалы времени системы GPS
фактическое время приема сигнала от i-го НКА, которое отличается от шкалы времени системы GPS
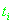 на величину
на величину
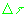 :
:
(4)
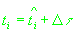 , ,
Связь истинной дальности
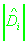 и измеренной псевдодальности
и измеренной псевдодальности
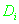 до i-го НКА в момент излучения сигнала определяется соотношением:
до i-го НКА в момент излучения сигнала определяется соотношением:
(5)
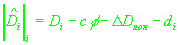 , ,
где
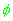 - ошибка в синхронизации часов приемника относительно шкалы времени системы,
- ошибка в синхронизации часов приемника относительно шкалы времени системы,
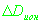 - ионосферная ошибка измерения,
- ионосферная ошибка измерения,
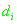 - случайная составляющая ошибки измерения псевдодальности,
- случайная составляющая ошибки измерения псевдодальности,
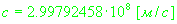 - скорость света.
- скорость света.
Для измеренного значения псевдоскорости
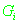 справедливо следующее соотношение:
справедливо следующее соотношение:
(6)
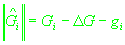 , ,
где
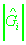 - истинное значение радиальной скорости,
- истинное значение радиальной скорости,
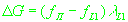 - величина, равная сдвигу частоты генератора НКА и гетеродина приемника,
умноженная на длину волны L1,
- величина, равная сдвигу частоты генератора НКА и гетеродина приемника,
умноженная на длину волны L1,
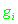 - случайная составляющая ошибки измерения псевдоскорости.
- случайная составляющая ошибки измерения псевдоскорости.
Рассмотрим инерциальную систему координат, направление осей которой совпадает с направлением осей подвижной системы координат WGS-84 на
момент времени
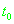 . Будем считать, что в некоторой окрестности момента регистрации сигнала связь вектора положения в системе WGS-84 и инерциальной
системе координат описывается следующем соотношением:
. Будем считать, что в некоторой окрестности момента регистрации сигнала связь вектора положения в системе WGS-84 и инерциальной
системе координат описывается следующем соотношением:
(7)
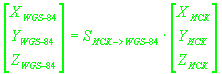 , ,
где 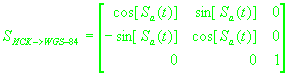 , ,
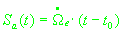 . .
Легко видеть, что соотношение для связи скоростей имеет следующий вид:
(8)
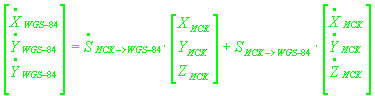 , ,
Вывод соотношений для обратного перевода очевиден, учитывая, что
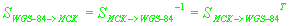 ,
. ,
.
Предположим , что в течение половины интервала
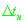 времени накопления сигнала скорость наблюдателя постоянна. Пусть
времени накопления сигнала скорость наблюдателя постоянна. Пусть
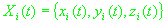 ,
,
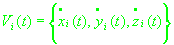 - положение и скорость i-го НКА в момент времени
- положение и скорость i-го НКА в момент времени
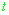 соответственно, а
соответственно, а
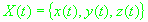 ,
,
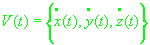 - положение и скорость наблюдателя в инерциальной системе координат.
Тогда подставив в (5) и (6) выражение истинной дальности и радиальной скорости
с учетом времени распространения сигнала и используя (4) получаем следующие соотношения:
- положение и скорость наблюдателя в инерциальной системе координат.
Тогда подставив в (5) и (6) выражение истинной дальности и радиальной скорости
с учетом времени распространения сигнала и используя (4) получаем следующие соотношения:
(9)
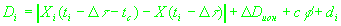 , ,
(10)
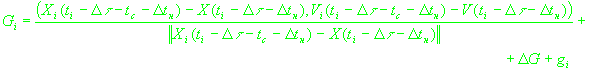 , ,
где -
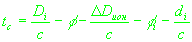 ,
время распространения сигнала. ,
время распространения сигнала.
Обозначим через
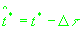 ,
момент одновременной регистрации измерений, тогда используя n одновременных измерений псевдодальности и
псевдоскорости можно составить следующую систему уравнений: ,
момент одновременной регистрации измерений, тогда используя n одновременных измерений псевдодальности и
псевдоскорости можно составить следующую систему уравнений:
(11)
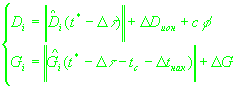 , ,
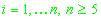 . .
Зная модель движения наблюдателя, и решив систему (11),
можно найти вектор положения
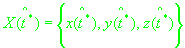 , вектор скорости
, вектор скорости
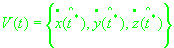 в инерциальной системе и неизвестные параметры:
в инерциальной системе и неизвестные параметры:
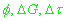 .
.
Система (11) решается в два этапа. Сначала находится приближенное решение системы, а потом при избыточности измерений оно уточняется методом
наименьших квадратов. Необходимо отметить, что система однозначно разрешима при количестве измерений не менее чем от пяти КА.
Предположим, что наблюдатель неподвижен. С учетом этого предположения положим
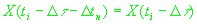 и
и
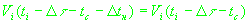 .
.
Определим положение наблюдателя и уточним ошибку в определении скорости за счет
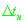 - разности по времени в регистрации измерений
псевдодальности и псевдоскорости.
- разности по времени в регистрации измерений
псевдодальности и псевдоскорости.
Пренебрегая учетом времени распространения сигнала и ионосферной ошибкой
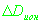 в уравнениях для псевдодальности системы (11), запишем систему
уравнений в виде:
в уравнениях для псевдодальности системы (11), запишем систему
уравнений в виде:
(12)
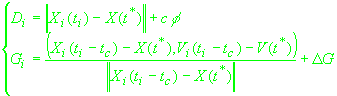 , ,
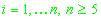 , ,
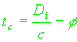 . .
Система (12) явно решается при наличии измерений от 4 НКА. Для ее решения используем алгоритм, предложенный в [4]. Необходимо отметить, что
первое уравнение системы (10) решается неоднозначно и в итоге мы имеем два решения системы:
(13)
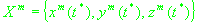 , ,
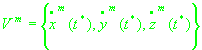 , ,
 , ,
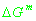 , ,
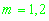 . .
Рассмотрим алгоритм устранения неоднозначности решения. Для этого используем измерения от пяти НКА следующим образом.
Для каждой четверки НКА из пяти имеющихся ищется два решения (13). Таких пар решений будет
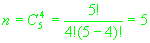 . Далее применим следующий
алгоритм разделения решений на два множества. На первом шаге алгоритма первая пара решений (13) распределяется по двум множествам произвольным
образом.
. Далее применим следующий
алгоритм разделения решений на два множества. На первом шаге алгоритма первая пара решений (13) распределяется по двум множествам произвольным
образом.
На k-ом шаге (k<5), получаем пару решений (13). Среди этих двух решений ищем то, у которого вектор положения
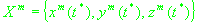 , ,
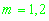 наиболее приближен к среднему одного из множеств. Найденное решение относим к этому множеству, а второе решение к другому множеству.
наиболее приближен к среднему одного из множеств. Найденное решение относим к этому множеству, а второе решение к другому множеству.
Итак, мы получили два множества со средними значениями компонент вектора положения, скорости и двух дополнительных искомых параметров
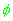 и и
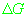 .
Из каждого множества удаляются те решения, у которых хотя бы одна компонента вектора положения или скорости лежит за пределами .
Из каждого множества удаляются те решения, у которых хотя бы одна компонента вектора положения или скорости лежит за пределами
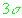 . Далее для
каждого множества вычисляется среднеквадратичная ошибка по каждому из параметров. Выбирается то множество, где модуль вектора среднеквадратичной
ошибки по положению меньше.
. Далее для
каждого множества вычисляется среднеквадратичная ошибка по каждому из параметров. Выбирается то множество, где модуль вектора среднеквадратичной
ошибки по положению меньше.
В качестве начального приближения решения системы (11) берутся средние значения компонент вектора положения, скорости,
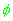 и и
 выбранного множества:
выбранного множества:
(14)
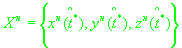 , ,
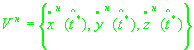 , ,
 , ,
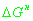 . .
По ходу проведения вычислительных экспериментов выяснилось, что значение
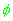 имеет порядок
имеет порядок
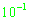 . Т.к. гарантированная точность одновременного приема сигнала имеет порядок
. Т.к. гарантированная точность одновременного приема сигнала имеет порядок
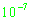 , то в качестве начального приближения поправки времени регистрации сигнала целесообразно использовать нулевое
значение, т.е.
, то в качестве начального приближения поправки времени регистрации сигнала целесообразно использовать нулевое
значение, т.е.
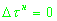 . .
Итак, мы получили приближенное решение системы (11) по одновременным измерениям не менее чем от 5 НКА.
Уточним найденное приближенное решение системы (11) методом наименьших квадратов [2]. Как и в случае с системой (12), пренебрежем ионосферной
ошибкой измерений и составим следующую систему:
(15)
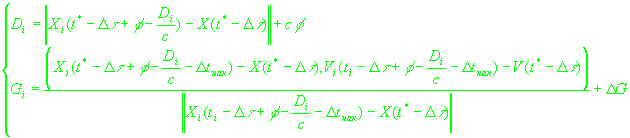 , ,
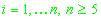 . .
Обозначим вектор неизвестных параметров через
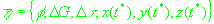 и и
(16)
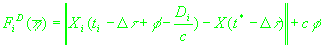 , ,
(17)
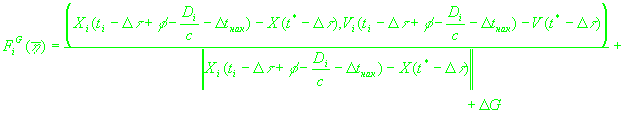 , ,
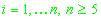 . .
Тогда вектор
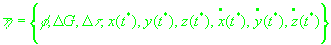 .
является решением системы (15) в смысле метода наименьших квадратов в том случае, если функция .
является решением системы (15) в смысле метода наименьших квадратов в том случае, если функция
(18)
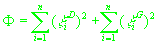
достигает своего минимума. Здесь
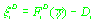 , ,
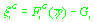 , ,
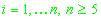 . .
Минимум функции (18) будем искать итерационным методом. На каждой итерации будем уточнять решение с использованием линейной модели. Найдем
параметры этой модели.
Пусть
(19)
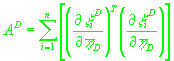 , ,
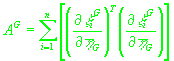 , ,
(20)
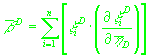 , ,
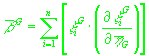 , ,
где
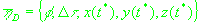 , ,
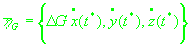 , ,
(21)
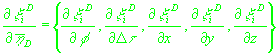 , ,
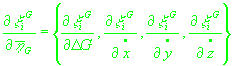 . .
Легко видеть, что:
(22)
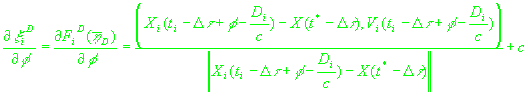 , ,
(23)
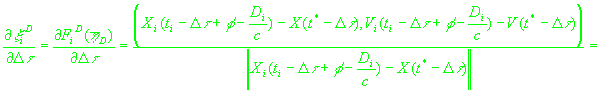
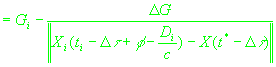 , ,
(24)
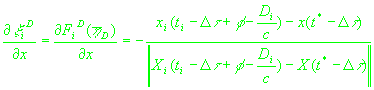 , ,
(25)
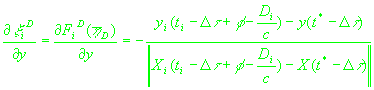 , ,
(26)
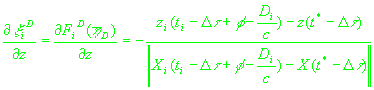 , ,
(27)
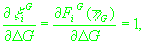 , ,
(28)
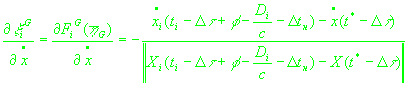 , ,
(29)
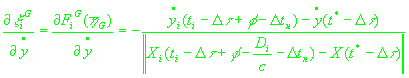 , ,
(30)
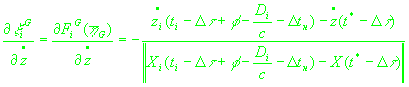 . .
В качестве нулевого приближения используем приближенное решение
(14)
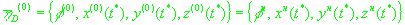 и и
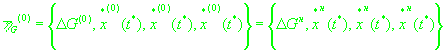 . .
Для начала итерационного процесса необходимо определить значения
следующих параметров:
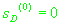 , ,
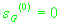 , ,
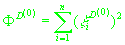 и и
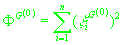 . .
Для каждой итерации выполняются следующие действия.
1. Последовательно решаются системы уравнений:
(31)
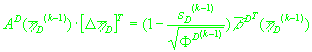 . .
(32)
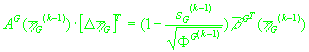 . .
2.
(33)
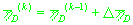 , ,
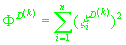 , ,
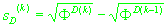 . .
(34)
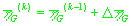 , ,
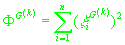 , ,
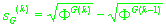 . .
3. Если
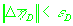 и и
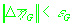 ,
где ,
где 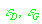 -
наперед заданные точности, то алгоритм завершается на шаге k, иначе происходит переход к следующему шагу. -
наперед заданные точности, то алгоритм завершается на шаге k, иначе происходит переход к следующему шагу.
В конце итераций мы получаем решение системы уравнений (15):
(35)
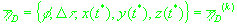 , ,
 . .
Таким образом, описан алгоритм, который позволяет по одновременным измерениям псевдодальности и псевдоскорости не менее чем от пяти НКА
определить вектор состояния наблюдателя, фазовый сдвиг псевдошумовой последовательности, смещение доплеровской частоты и время регистрации
сигнала.
Назад | Оглавление | Далее
Версия PDF:
ftp://ftp.kiam1.rssi.ru/pub/gps/lib/publications/preprint36_01.pdf
|